Need to calculate sett for an unfamiliar yarn? Ashenhurst’s Rule will help. In this blog post and its sequel, we’ll explain how Ashenhurst’s rule works and how you can apply it in your weaving.
What is Ashenhurst’s Rule?
Thomas R. Ashenhurst (1849-1902) was the chief instructor in weaving and pattern designing at the Bradford Technical College in West Yorkshire, England in the 1880s and 90s. In the course of writing several books, he compiled charts and mathematical equations useful to weavers of his time – and ours!
To help solve one of the thorny problems of the day, Ashenhurst came up with a formula for determining the maximum possible sett for a fabric. His formula is based not on the subjective process of wrapping yarn around a measuring device Just So, but on an objective number: the yards per pound of the yarn used for warp and weft.
Show me the formula!
There are actually two equations that make up Ashenhurst’s formula. If you’re only here to get the equations and run, here they are:
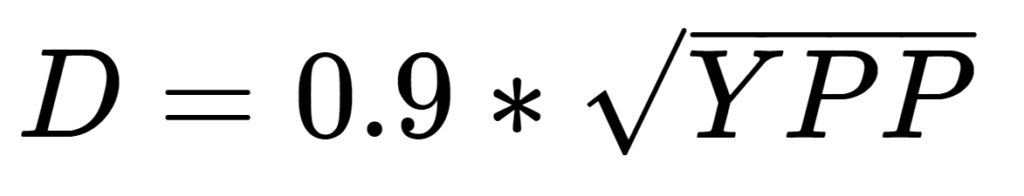
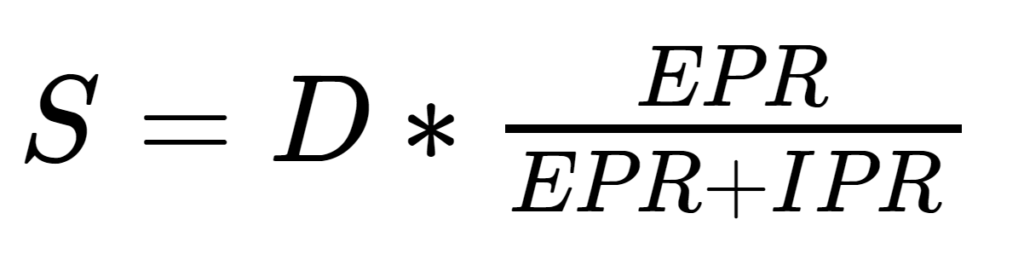
YPP is the number of yards per pound
D is the number of diameters per inch
EPR is the ends per repeat
IPR is the number of intersections per repeat
S is the maximum sett possible with the yarn in the structure
That 0.9 multiplier assumes that the yarn in question is dense rather than lofty. If it’s lofty, Ashenhurst recommends using 0.84 instead.
Confused? Don’t worry! The purpose of this post is to explain Ashenhurst’s equations so that you can use his formula yourself..
(Don’t want to do the math? We have a handy Ashenhurst calculator that does it all for you! Plus lots of other tools, such as the Draft Editor and Twill Generator, inside the Academy.)
The next lessons explain what all those numbers mean, how to find them, and then how to plug them into the equation – or, if you’re a member, into our Ashenhurst Calculator.
The cheat sheet for plain weave and four shaft twill
Having said that, if you happen to be weaving plain weave or a twill on four shafts, then you can safely skip the complicated stuff related to EPR and IPR. Just calculate S using one of the following equations.
The equation for plain weave:
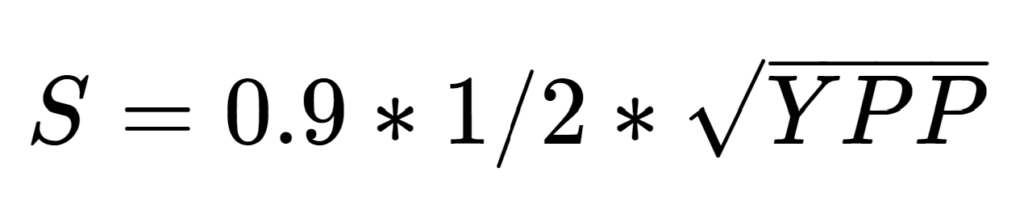
The equation for a twill threaded on four shafts:
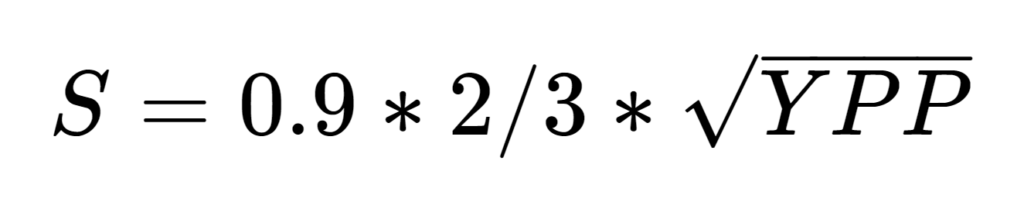
IMPORTANT: the number produced is the maximum possible sett, not the recommended sett! In our next blog post, we’ll explain how to choose a more reasonable sett.
What does his formula tell you?
Ashenhurst’s equations tells you two things:
- D = the number of yarn diameters that fit into an inch, and
- S = the maximum number of warp ends and weft picks that can be jammed into a single inch of fabric with a particular structure.
Note that the second thing is the maximum possible sett, NOT a recommended sett!
For one thing, it would be very difficult to achieve this sett: you’d have to pound the heck out of each and every weft pick to bash it into place and then keep it there. For another, fabric this dense would be very, very stiff.
If your goal IS a very dense and stiff – and durable! – fabric, then you might want to use a sett close to Ashenhurst’s maximum. For most purposes, however, a lower percentage of this maximum is a more appropriate choice. We’ll talk about reasonable percentages in our next post.
Why is his formula useful?
If it doesn’t give you a usable sett directly, is Ashenhurst’s formula really of any use? Yes, certainly!
It gives you more objective results
The first thing it tells you is the number of yarn diameters that fit into an inch. This is just another way of saying “wraps per inch”. The advantage of using Ashenhurst’s formula rather than wrapping around a ruler is that it’s not as subjective. There’s no worry about whether you’re pulling the yarn too much, or squeezing the wraps too close together or not close enough. Using Ashenhurst’s formula to determine diameters (wraps) per inch means you can’t really go wrong.
It’s useful in more situations
Ashenhurst’s formula is also useful when the yarn is just too fine to make wrapping around a ruler practical. Wrapping a knitting yarn around a ruler might not be difficult, but imagine trying to do the same with sewing thread or 120/2 silk!
It takes structure into account
Ashenhurst’s formula also takes the actual interlacement of threads into account more precisely than the usual “use half for plain weave, or two thirds for twill”. 2/3rds may be just right for four shaft twills, but twills on more shafts have different ratios and need a different multiplier.
WHEN is his formula useful?
Ashenhurst designed his formula for cloth that
- has just one warp and one weft,
- has the same yarn for warp and weft, and
- is balanced, with the same number of warp ends and weft picks per inch/cm.
If your plans don’t meet these restrictions, you can still use his formula to decide on a good starting point for sampling. We’ll cover how later in this post.
A note about units of measurement
Ashenhurst came up with these equations in the late 1800s, long before the metric system was adopted in England. In fact, many of his equations came about precisely because units of measurement in the textile industry were far from standardized – even the practice of measuring sett in ends per inch wasn’t widely accepted yet!
Fun fact: at the time, many mills measured sett in “beers”, which were a certain number of ends (the number varied) in a given width (which also varied). I imagine if we were still measuring things in beers, our calculations would vary, too!
Because Ashenhurst’s equations depend on imperial units, this post uses yards per pound and ends per inch throughout for calculations. If you use metric units and want to actually perform the calculations yourself, you’ll need to convert back and forth.
(For members, the metric version of our Ashenhurst calculator conveniently takes inputs in meters per kilogram and returns setts in ends per centimeter.)
What do you need to use Ashenhurst’s formula?
If you’re planning to weave plain weave or a four shaft twill and you’re willing to take the rest on faith, all you really need is yards per pound so you can calculate D. For the fraction in the second equation, just use 1/2 for plain weave and 2/3 for your four shaft twill.
If you’re not weaving plain weave or four shaft twill, you need three pieces of information to use Ashenhurst’s formula to calculate an appropriate sett:
- The yards per pound of the yarn you’re going to use
- The number of ends and picks in a single repeat
- The number of intersections in that same repeat
YPP: Yards per pound
The first and most important number you need to plug into the formula is the yarn’s yards per pound. If it’s a commonly used weaving yarn, chances are good that you can look up this information in Handwoven’s Master Yarn Chart.
EPR: the number of ends in a threading repeat
The next thing you need to know is the number of ends in one threading repeat.
Color doesn’t matter for our purposes, so you can ignore any stripes or colors and just operate as if your warp and weft are all one color. Easy!
Note that the length of the threading repeat can vary from one draft to the next, even for the same structure! These are both plain weave drafts, but the threading repeat is 2 ends in the first and 4 ends in the second:
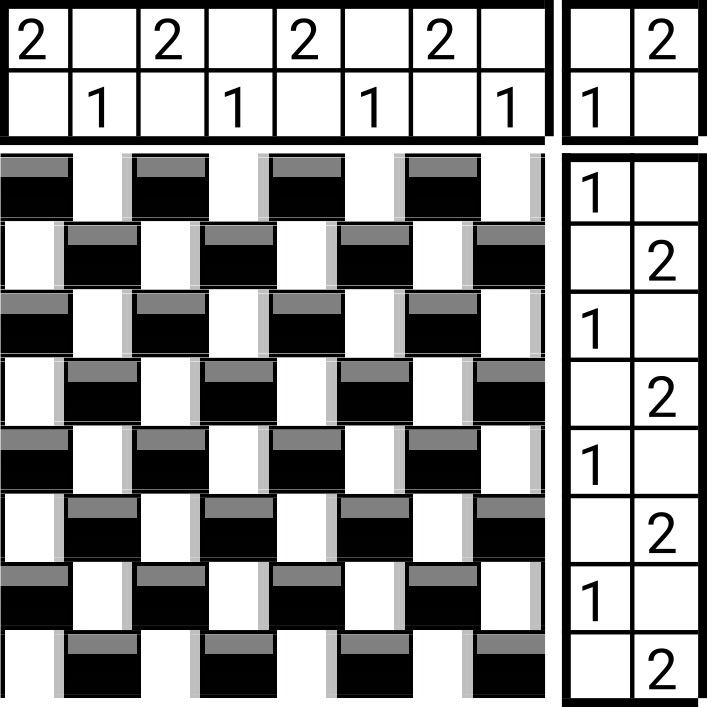

IPR: the number of intersections in a threading repeat
The last number you need to use Ashenhurst’s formula is the number of intersections in a single repeat. That’s a more complicated number to figure out, but we’ll explain how in the next blog post.

