There are lots of denting charts online (often called reed or sett substitution charts) but in my opinion a chart just doesn’t cut it. For one thing, there are often entries missing. Want to know how to get 22 EPI in a 10 dent reed, or 17 EPI in an 9 dent reed? Good luck finding a chart that includes those options!
For another, charts don’t explain the math behind the calculations, which means you stay dependent on the chart to provide magical answers. The math isn’t tricky, so there’s no reason you can’t be independent and work out exactly how to get the sett you want in the reeds you already own.
Our denting calculator – which members can find in the Weavers Toolbox, will tell you how to get any sett from any reed.
If all you need at This Moment Right Now is that answer, then by all means head to the calculator and get what you need so that you can carry on with your project! To learn how to do the math yourself, read on:
How to sley for any sett in any reed
Calculating how to sley a particular number of ends per inch (EPI) in a reed with a given number of dents per inch (DPI) is actually very simple:
- Divide the EPI by the DPI – long hand, to get a quotient and a remainder. Leave the remainder, if any, as a fraction.
- Reduce the remainder as far as possible.
- The whole part of the answer is the number of threads to put in every dent.
- The fraction tells you how many dents (the numerator) out of how many dents (the denominator) get an extra thread.
The math is exactly the same for metric, just use ends per cm (or 10cm) and dents per cm (or 10cm).
Example 1: 20 EPI in a 12 dent reed
Say you have a 12 dent reed and you need to sley it at 20 ends to the inch. That means you need to divide 20 (the EPI) by 12 (the DPI):
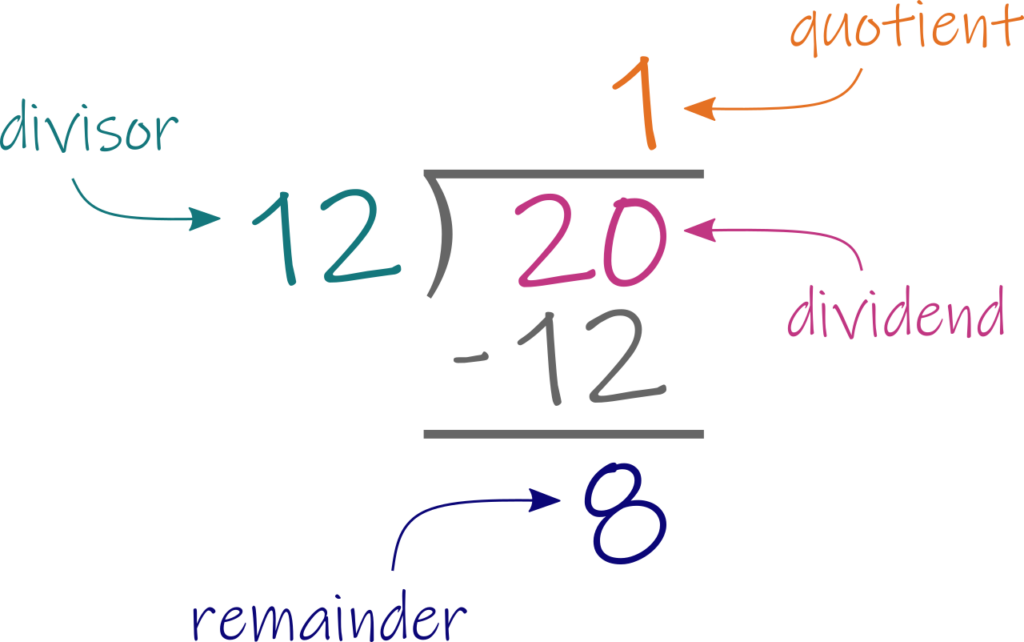
The quotient is 1, the remainder is 8, and the divisor is 12, so the answer to this long division problem is 1 8/12. That can be reduced to 1 2/3.
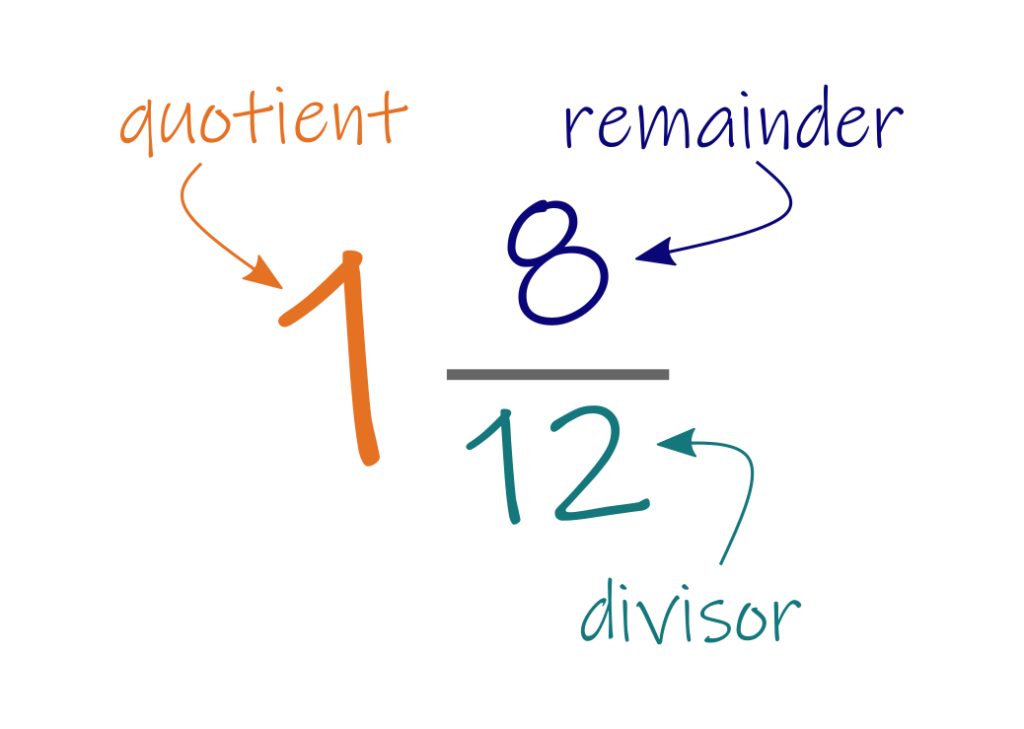
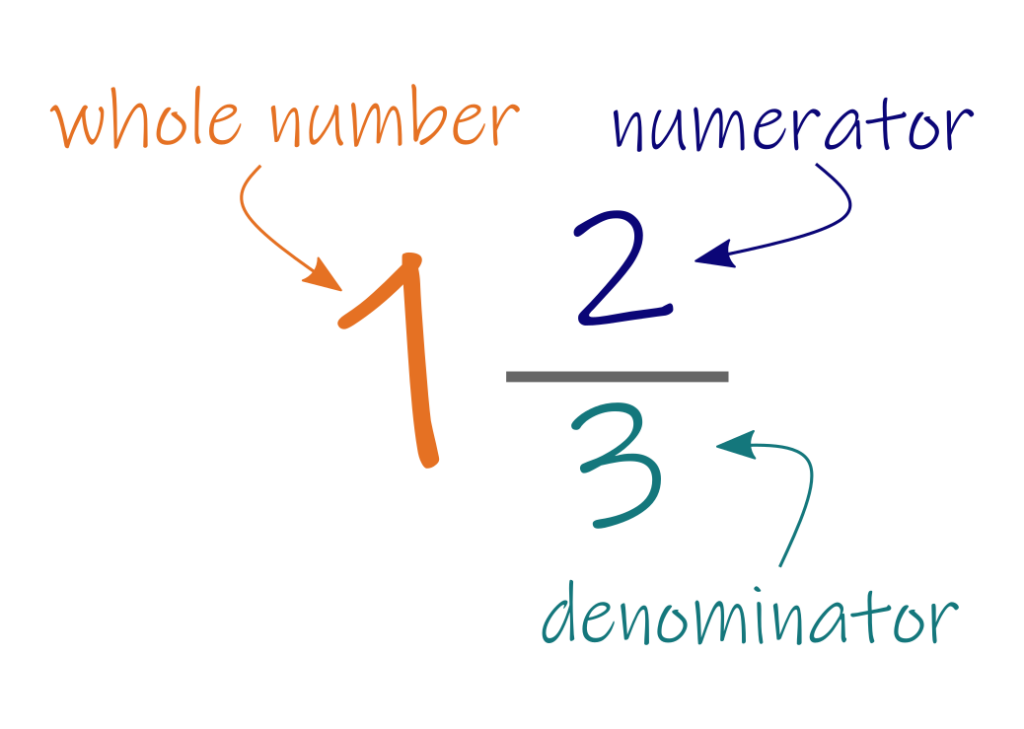
Remember:
- The whole part of the answer is the number of threads to put in every dent.
- The fraction tells you how many dents (the numerator) out of how many dents (the denominator) get an extra thread.
So in this example, every dent gets one thread (the quotient) and two dents out of every three get one more thread.
What does this look like in the reed?
The quotient – in this case, 1 – is the number of ends that goes in every dent:
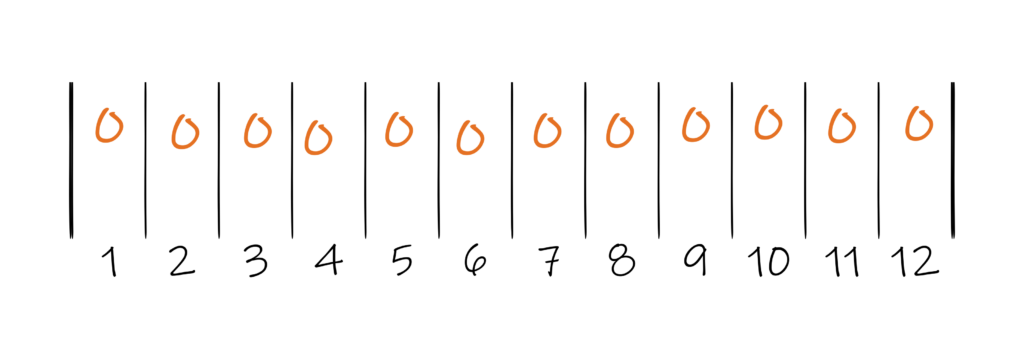
Then you take those same dents in groups the size of the fraction’s denominator – in this case, 3:
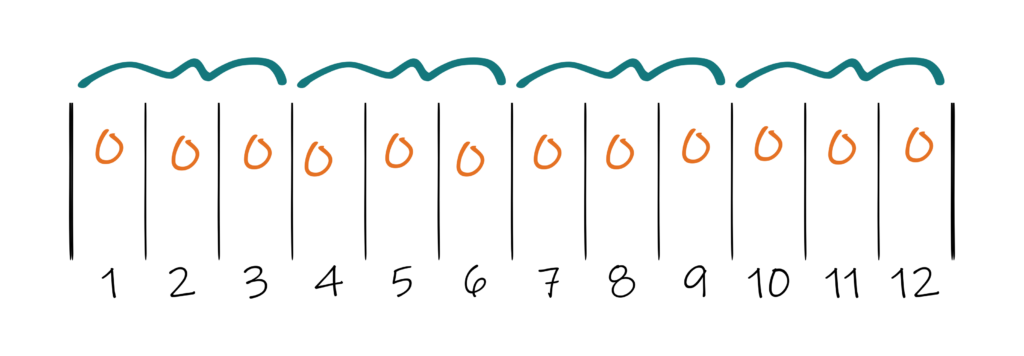
And in each of those groups, a number of dents equal to the fraction’s numerator – in this case, 2 – gets an additional end:
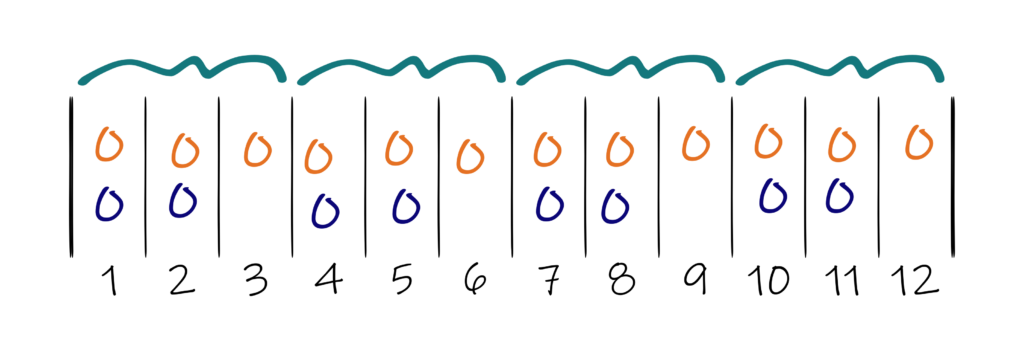
It doesn’t matter which two of the three dents get the extra end (for a total of two ends per dent) and which doesn’t but it’s a good idea to follow the same pattern all the way across. Note that there are eight extras per 12 dents, just like our original, UNreduced remainder.
The equivalent to this on most reed substitution charts would be 2-2-1. Or, more likely, 1-2-2, since reed substitution charts usually start with the fewer number of ends per dent. Either way, it means the same thing: two of the three dents get two ends and the third gets just one.
Example 2: 8 EPI in a 12 dent reed
Nothing changes if EPI is less than DPI. If you want 8 ends per inch in a 12 dent reed, you do the long division exactly like before…
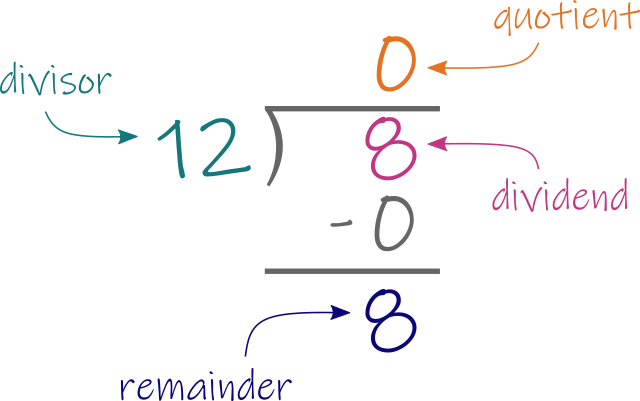
…but now the quotient is zero because the divisor is bigger than the dividend. The next step is still to reduce the fraction in the answer:
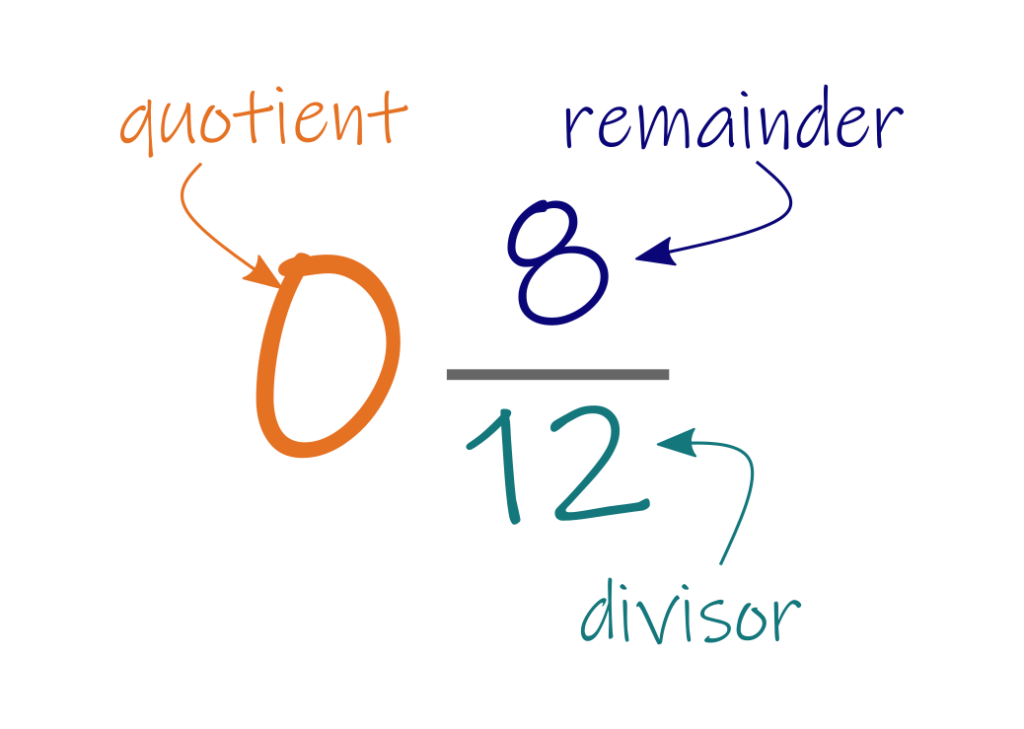
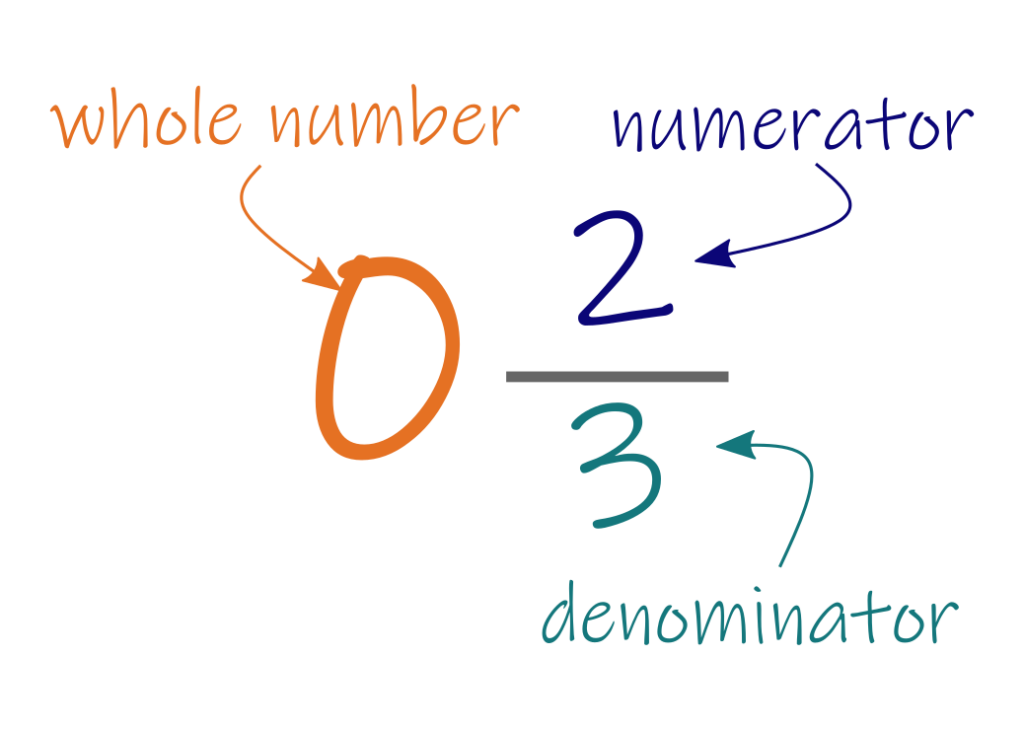
And then you apply the logic, i.e.
- The whole part of the answer is the number of threads to put in every dent.
- The fraction tells you how many dents (the numerator) out of how many dents (the denominator) get an extra thread.
Because the whole number is zero, every dent gets zero threads as a “base amount.” Because the fraction is still 2/3s, two dents out of every three still get one more thread in addition to the base.
What does this look like in the reed?
The quotient – in this case, 0 – is the number of ends that goes in every dent:
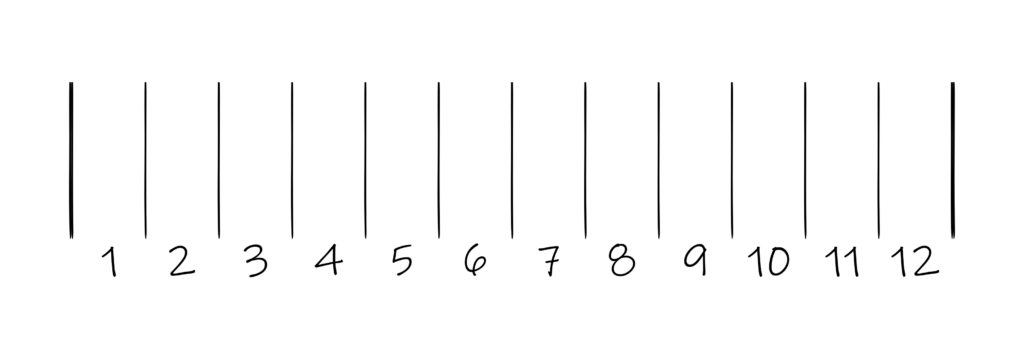
Then you take those same dents in groups the size of the fraction’s denominator – in this case, 3:
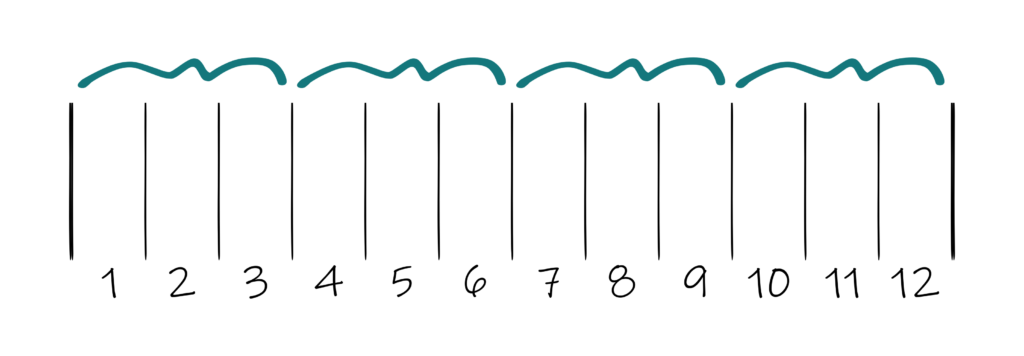
And in each of those groups, a number of dents equal to the fraction’s numerator – in this case, 2 – gets an additional end:
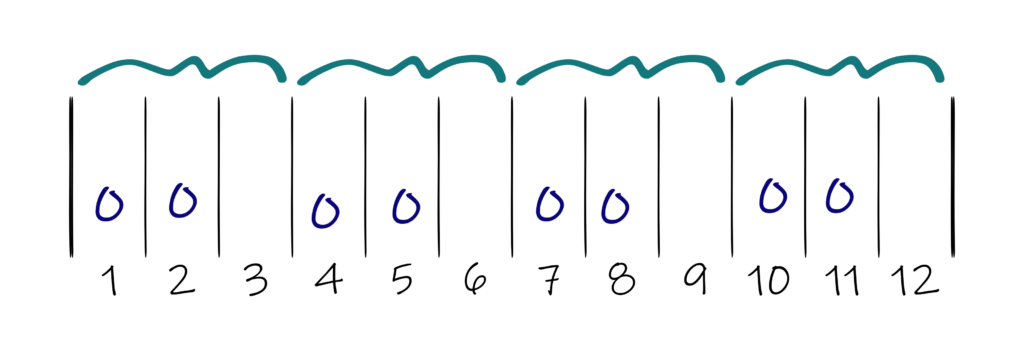
And there you have it: eight ends spread across 12 dents, which equals one inch, or 8 EPI in a 12 dent reed.
The equivalent to this on most reed substitution charts would be 1-1-0. Or, more likely, 0-1-1, since reed substitution charts usually start with the fewer number of ends per dent. Either way, it means the same thing: two of the three dents gets one end and the third dent is empty.
Now you have the tools to get a quick answer, or work the answer out yourself!
Happy Sleying!
From the Course Catalog:
Ashenhurst’s Formula to Determine Sett – take the guesswork out of chooseing a sett
From the Weavers Toolbox:
